Skyline アルゴリズムで実現するグリッドを超えた柔軟なレイアウト

• 2025年6月23日
• Bin Packing,
• データ構造・アルゴリズム

CSS Grid や Flexbox により、CSS だけで表現できるレイアウトの幅が広がりました。しかし、グリッドの枠を超える柔軟な UI は CSS のみでは実装が困難です。例えば、短いメモと画像を二次元に並べる以下の UI は CSS Grid や Flexbox だけでは表現できません。

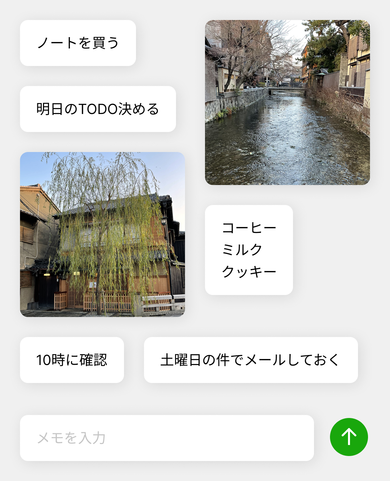
CSS Grid も Flexbox も行や列を定義し、その中に要素を配置するため、行や列にとらわれない UI の実装は困難です。よく使用される Masonry レイアウトは Grid より自由度が高いものの、列か行の片方を厳密に並べるため柔軟性に欠けます。

本記事では Skyline アルゴリズムがこのような柔軟な配置を実現できることを示します。基本的なアルゴリズムを紹介した後、より多くの空きスペースを削減し、より美しいレイアウトを作るための拡張も解説します。

Skyline アルゴリズム #

Skyline アルゴリズムは二次元ビンパッキング問題の近似解を求めるアルゴリズムです。ビンパッキング問題とは、様々な大きさの矩形を決められた空間（ビン）に効率よく詰め込み、使用するビンの数を最小化する問題です。応用例として、ゲームのテクスチャをスプライトシートにまとめる処理があります。

本記事では Skyline アルゴリズムを縦方向に無限に伸びる UI に応用します。幅は固定で高さは無限の1つのビンに詰め込む実装とします。

スカイラインとは #

Skyline アルゴリズムの核心は、配置済み矩形の上端が作る輪郭線をスカイラインとして管理することです。スカイラインは都市のビル群が空に描く輪郭線のことです。新しい矩形はスカイライン上の最も低い位置に配置します。以下はスカイラインを図示したものです。Web の座標系とは異なり Y 座標の原点は下にあります。

スカイラインは座標点の配列として表現し、X 値でソートします。最も左の点と Y 座標が変化する点に着目します。

このスカイラインは以下の配列で表します。

skyline = [(0, 5), (7, 7), (9, 4)]

矩形の配置アルゴリズム #

以下のクラスで Skyline アルゴリズムを実装します。初期状態のスカイラインは高さ 0 で平坦です。

class SkylinePacker {
  /** ビンの幅 */
  #width

  /** 配置済み矩形の配列 */
  #packedRectangles = []

  /** スカイライン（初期高さ 0） */
  #skyline = [{ x: 0, y: 0 }]

  constructor(binWidth) {
    this.#width = binWidth
  }

  getRectangles() {
    return this.#packedRectangles
  }

  // 以下に処理を追加
}

矩形はスカイライン上の最も低い位置に配置します。

矩形同士の重なりは禁止されているため、他の矩形と重なる場合は、重ならなくなるまで Y 座標を増加させます。下図では二番目の矩形の上に横長の矩形を配置しようとしていますが、三番目の矩形と重なるため Y 座標を増加させています。ただし、Y を増加させた後の配置はあくまで候補なので、より低い位置に配置できる場合はそちらを優先します。

以下がコード実装です。結果には採用したスカイライン点のインデックス（index）と削除する点の数（removeCount）を含めます。これらは次節のスカイライン更新処理で使用します。

/**
 * 矩形を配置する座標を計算。
 * 結果には配置位置のスカイライン点の index と、スカイライン更新時に削除すべき点の数を含める。
 */
#getPlacementPosition(item) {
  let bestPosition = null

  for (let i = 0; i < this.#skyline.length; i++) {
    const node = this.#skyline[i]
    const x = node.x

    // ビン幅を超える場合はスキップ
    if (x + item.width > this.#width && bestPosition) {
      continue
    }

    // 初期 Y 座標
    let y = node.y

    // 後方のスカイライン点で重なりチェック
    // 重なる場合はYを調整
    let j = i + 1
    for (; j < this.#skyline.length; j++) {
      const currentNode = this.#skyline[j]

      if (currentNode.x >= x + item.width) {
        break
      }

      y = Math.max(y, currentNode.y)
    }

    // より小さい Y 座標に配置できるときはそれを採用
    if (!bestPosition || y < bestPosition.y) {
      bestPosition = {
        x,
        y,
        index: i,
        removeCount: j - i,
      }
    }
  }

  return bestPosition
}

外側の for ループで左から順にスカイライン点への配置を試みます。内側の for ループでは右側のスカイライン点をチェックし、他の矩形との重なりを確認します。スカイライン点は配置済み矩形から決まるため、スカイラインのチェックだけで重なりを判定できます。

スカイラインの更新アルゴリズム #

矩形配置後はスカイラインを更新します。以下の2つの処理をおこないます。

• 矩形の配置で無効となる点の削除
• 配置された矩形で上昇する輪郭を表す点の追加

スカイライン点の削除は、配置した矩形の幅が下の矩形より大きい場合に発生します。下図では新しい矩形が下の矩形を覆うため、下の矩形の右端のスカイライン点を削除します。

矩形配置時は左端のスカイライン点を削除し、Y 座標を矩形の上端に更新したものを追加します。矩形の右下にも点を追加する場合があります。下図で示したケースのように、矩形の右端に既存のスカイライン点がある場合、右端の点は追加しません。

以下はスカイラインの更新処理をコードで表したものです。

/**
 * 矩形配置とスカイライン更新
 */
placeItem(item) {
  // 前節の処理で矩形の配置座標を計算
  const position = this.#getPlacementPosition(item)

  // 無効となる点を削除
  const removed = this.#skyline.splice(position.index, position.removeCount)
  const lastRemoved = removed[removed.length - 1]
  const next = this.#skyline[position.index + 1]

  // 左端の新しいスカイライン点
  const leftNew = {
    x: position.x,
    y: position.y + item.height
  }

  // 右端の新しいスカイライン点
  const rightNew = {
    x: position.x + item.width
    y: lastRemoved.y,
  }

  // 左端の点を追加
  this.#skyline.splice(position.index, 0, leftNew)

  // 右端の点は条件を満たす場合のみ追加
  if ((!next || rightNew.x < next.x) && rightNew.x < this.#width) {
    this.#skyline.splice(position.index + 1, 0, rightNew)
  }

  // 配置結果を保存
  this.#packedRectangles.push({
    width: item.width,
    height: item.height,
    x: position.x,
    y: position.y,
  })
}

前節で計算した index と removeCount により処理が簡潔になります。配置計算時に重なると判定されたスカイライン点は削除対象なので、その結果を更新処理に活用できます。

先読みによる空きスペースの最小化 #

基本的な Skyline アルゴリズムは、各矩形をその時点の最適位置（Y 座標が最小の位置）に配置する貪欲法です。しかし、幅の長い矩形の後に短い矩形がある場合、長い矩形により空きスペースが生じ、短い矩形を配置できなくなります。以下の図では、画像の下の長いメモにより、後続の短いメモが画像横のスペースに配置できません。

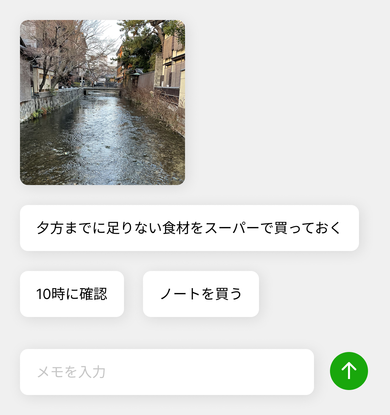
この問題を 先読み（Look Ahead） で解決します。次の矩形の配置位置が現在のスカイライン内で最小の Y でない場合、後続の矩形の配置を試し、空きスペースに収まる場合はそれを先に配置します。今回例として挙げているメモと画像を並べる UI では、ユーザーにとって並び順が厳密である必要はなく、大まかな順序が保持されていれば良いと考えられます。先読みで局所的に順番を変えて、空間の有効活用と見た目の美しさを優先する選択もありでしょう。

実装では、矩形の配列と先読み数を受け取り、次に配置する矩形のインデックスを返す #findBestItemIndex 関数を作ります。空きスペースに収まる矩形が見つかればそのインデックスを、見つからなければ 0 を返します。

/**
 * 先読みでより小さい y 座標に配置できる矩形を探す。
 * 次に配置すべき矩形の index の値を結果として返す。
 */
#findBestItemIndex(items, lookAheadSize) {
  const windowSize = Math.max(1, Math.min(lookAheadSize + 1, items.length))
  const window = items.slice(0, windowSize)

  // 最初の矩形の配置位置を基準とする
  const firstPlacement = this.#getPlacementPosition(window[0])
  const baselineY = firstPlacement.y

  let bestChoice = {
    index: 0,
    score: firstPlacement.y
  }

  // 先読み範囲で探索
  for (let i = 1; i < window.length; i++) {
    const item = window[i]
    const placement = this.#getPlacementPosition(item)

    // baselineY 以下で最も低い位置に配置できる矩形を探す
    if (placement.y + item.height > baselineY) {
      continue
    }

    // より小さい Y 座標に配置できるときはそれを採用
    if (placement.y < bestChoice.score) {
      bestChoice = {
        index: i,
        score: placement.y
      }
    }
  }

  return bestChoice.index
}

そして #findBestItemIndex と前節で実装した placeItem を組み合わせた placeItems 関数を作ります。先読みで次の矩形を選び、配置します。

placeItems(items, lookAheadSize = 2) {
  const remainingItems = [...items]

  while (remainingItems.length > 0) {
    // 先読みで次の矩形を選択
    const bestIndex = this.#findBestItemIndex(remainingItems, lookAheadSize)

    // 矩形を取得
    const chosenItem = remainingItems.splice(bestIndex, 1)[0]

    // 配置実行
    this.placeItem(chosenItem)
  }
}

配置制約への対応 #

UI デザインでは、要素を特定のグリッドに沿って配置したい場合があります。メモ UI の例では、正方形の画像を左右2カラムに制約すると見た目が整います。制約なしでは画像の配置が中途半端になり、空きスペースが生じたり、整頓されていない印象を与えます。

このような要件に対応するため、各矩形の配置時に xConstraints を指定できるようにします。xConstraints は配置可能な X 座標の配列です。例えば、xConstraints: [200, 400] と指定します。実装では、スカイラインに制約の X 座標を挿入し、その点でのみ配置を試みます。

#getPlacementPosition の先頭にスカイライン更新処理を追加します。制約で追加される点の Y 座標は、左側の既存点の Y 座標を使用します。

// #getPlacementPosition の先頭に追加
// 矩形の配置位置を計算する前に、制約に対応する位置にスカイライン点を追加

const xConstraints = item.xConstraints ?? []

// 制約点をスカイラインにマージ
if (xConstraints.length > 0) {
  const sortedXConstraints = [...new Set(xConstraints)].toSorted(
    (a, b) => a - b,
  )
  const newSkyline = []

  let xConstraintsIndex = 0
  let skylineIndex = 0

  // 制約と既存点をマージ
  while (
    xConstraintsIndex < sortedXConstraints.length ||
    skylineIndex < this.#skyline.length
  ) {
    const constraintX = sortedXConstraints[xConstraintsIndex]
    const skylineNode = this.#skyline[skylineIndex]

    if (
      skylineNode === undefined ||
      (constraintX !== undefined && constraintX < skylineNode.x)
    ) {
      // 制約点を挿入（Yは前の点から取得）
      const prevY = newSkyline[newSkyline.length - 1]?.y ?? 0
      newSkyline.push({
        x: constraintX,
        y: prevY,
      })

      xConstraintsIndex++
    } else {
      // 既存点を保持
      newSkyline.push(skylineNode)

      skylineIndex++

      // 重複点は制約も消費
      if (constraintX === skylineNode.x) {
        xConstraintsIndex++
      }
    }
  }

  this.#skyline = newSkyline
}

配置探索ループ内で、制約に対応しないスカイライン点をスキップします。

// #getPlacementPosition の for ループの中を更新

for (let i = 0; i < this.#skyline.length; i++) {
  const node = this.#skyline[i]
  const x = node.x

  // 制約がある場合は制約点のみ使用
  if (xConstraints.length > 0 && !xConstraints.includes(x)) {
    continue
  }

  // 以下同様の配置を探す処理
}

配置後のスカイライン更新では xConstraints の特別な処理は不要です。制約で追加された点は次の配置でも引き継がれますが、Y 座標が同じ場合は左側を優先するため挙動は変わりません。メモリ使用量の増加は軽微で、スカイラインの更新処理でいずれ削除されるため、動作に影響はないでしょう。

拡張 Skyline アルゴリズムのデモ #

以下はこれまで解説した拡張 Skyline アルゴリズムのデモです。「次の矩形を追加」ボタンで矩形を追加でき、アルゴリズムの動作を確認できます。矩形の数字は元の順番を示します。先読みサイズを変えると、空きスペースを埋めるための順番変更が確認できます。

結論 #

本記事では、CSS Grid や Flexbox だけでは表現できない柔軟なレイアウトを実現する Skyline アルゴリズムを解説しました。このアルゴリズムは配置済み矩形の上端が作るスカイラインを管理し、その中から最も低い位置に新しい矩形を配置するというシンプルなアイデアに基づいています。

基本的な Skyline アルゴリズムは貪欲法で矩形を配置しますが、長い矩形による空きスペースを活用できません。先読みを導入し、後の矩形が空きスペースに収まる場合は順番を入れ替えて効率的に配置します。

配置制約も実装しました。xConstraints で矩形を特定のグリッドに沿って配置でき、整頓されたレイアウトが作れます。

Skyline アルゴリズムはビンパッキング問題の解法として知られていますが、本記事で示したように UI レイアウトにも応用できます。グリッドを超えた柔軟な配置の選択肢として覚えておくと良いでしょう。

参考文献 #

• Jukka Jylänki, "A Thousand Ways to Pack the Bin - A Practical Approach to Two-Dimensional Rectangle Bin Packing"
• The Skyline algorithm for packing 2D rectangles