iOS のスプリングを CSS 数式アニメーションで再現する

2023年10月16日
アニメーション,
iOS,
CSS

「こういうアニメーションを作ってると未来予知したくなるんですよね」

9月30日の複雑 GUI 会に参加した時に、「iOS のラバーバンドスクロールを Web で実装する方法」のラバーバンド実装を見せた時にこんな事を言いました。物理演算を取り入れたアニメーションはフレームごとに次の位置を計算するため、例えば1秒後にどこにいるのかを事前に知ることはできないので、数式を使って計算したくなるという話でした。

この話をしたら、参加者の方に WWDC 2023 で発表された Animate with springs を教えていただきました。iOS では、従来物理演算で行われていたスプリングアニメーション（Spring Animation）を数式で表現していることが解説されていて、実際の数式も紹介されており、とても興味深いものでした。

数式によるスプリングアニメーションの実装を Web に持ってこれたらおもしろいのではないかと思い、何度も動画を視聴し、数式の理解を試みました。ある程度 Web で動かせるようになるまで理解が進んだので、本記事ではその数式の解説と、簡単な実装の紹介をします。

従来のスプリングアニメーションはパラメーターがわかりづらい #

JavaScript でもスプリングアニメーションを実装した数々のライブラリがありますが、どれも物理演算を元にしたパラメーターを使ってアニメーションを設定します。例えば、物体の重さを表す mass、バネの引っ張る強さを表す stiffness、物体の速度が落ちる度合いを表す damping が使われます。開発者が表現したいアニメーションにするために、これらのパラメーターにどんな値を設定すればいいかは直感的にわかりづらいです。

// 一般的なスプリングアニメーションライブラリの設定のイメージ
// mass, stiffness, damping の値によってどのようにアニメーションするのかわかりづらい
const springValue = spring(
  { from: 0, to: 10 },
  {
    mass: 1,
    stiffness: 100,
    damping: 10,
  },
)

iOS では数式による実装でパラメーターをわかりやすくしている #

Animate with springs では、iOS のアニメーションでは物理演算ではなく、数式を元にしたアニメーションを行っていることが説明されています。アニメーションのパラメーターにはバウンスの度合いを表す bounce とアニメーションの時間を表す duration の2つのみを指定すれば良く、直感的にわかりやすいです。

// bounce と duration だけで設定するスプリングアニメーションのイメージ
// 少しバウンスして、800ms かけてアニメーションすることが想像できる
const springValue = spring(
  { from: 0, to: 10 },
  {
    bounce: 0.2,
    duration: 800,
  },
)

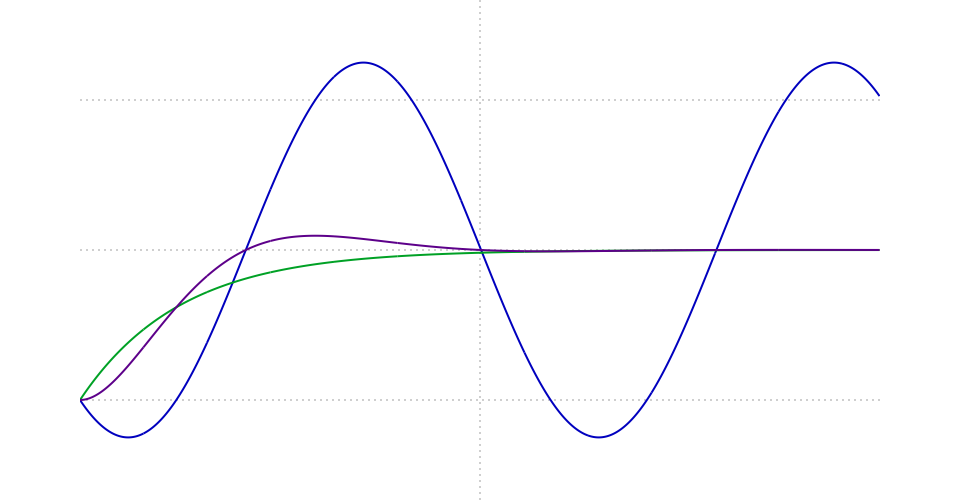
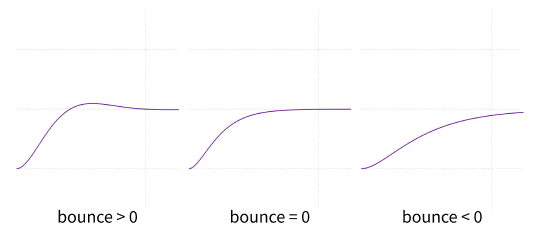
iOS では bounce の値によって異なる数式を使っていることが説明されています。以下は bounce の値によってどのようなアニメーションになるかを表したグラフです。bounce > 0 の時は終了位置を越えてから跳ね返って戻るアニメーション、bounce = 0 の時は跳ね返りがなく自然に終了位置に向かっていくアニメーション、bounce < 0 の時はよりフラットな動きをするアニメーションとなります。

bounce の違いによるグラフの比較

数式はバウンス部分と減衰部分に分けられる #

本記事では bounce > 0 の時の数式を解説します。bounce > 0 の時は以下の数式が使われます。

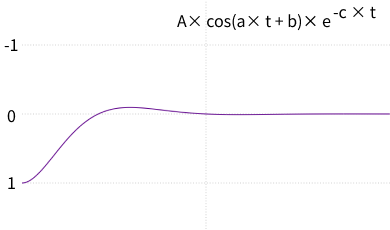
A × cos(a × t + b) × e ^{-c × t}

A, a, b, c は定数、e はネイピア数、t はアニメーションの経過時間（0 が開始、1 が duration で設定した時間が経過した時）です。この数式全体を評価した時の値が、アニメーション対象の位置を表します。この数式をグラフにすると以下のようになり、スプリングアニメーションの動きがイメージできます。

スプリングアニメーションの数式のグラフ

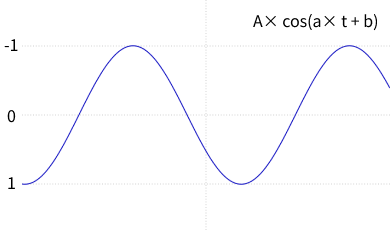
この数式のアイデアは、バウンスを表現する部分と、減衰を表現する部分の2つの数式をかけあわすことです。bounce > 0 の時、アニメーションの対象は終了位置を軸に振動します。この振動を cos 関数で実現しています。

cos 関数のグラフ

cos 関数をそのまま使うだけでは永遠に振動し続けるので、この振動を減衰させる必要があります。減衰には指数関数を用いています。指数部分を負の数にすることで、t = 0 の時は減衰がなく、時間がたつにつれて減衰量が大きくなっていきます。

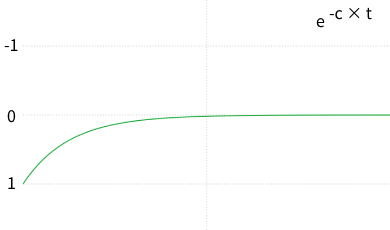
指数関数のグラフ

この指数関数と cos 関数をかけあわせることで、振動が減衰しながら終了位置に収束する動きを表現できます。

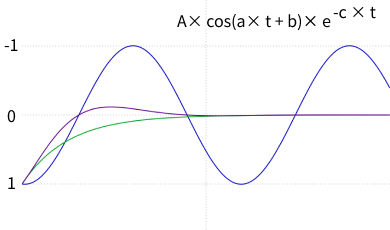
指数関数と cos 関数をかけあわせたグラフ

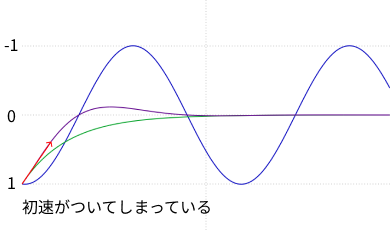
これだけでかなりスプリングアニメーションの動きとしては良い感じになりますが、初速がついてしまっています。ほとんどの場合、速度が 0 の状態からアニメーションを始めるため、自然な印象を与えるために、速度が 0 から連続的に変わるようにグラフを修正する必要があります。

かけあわせたグラフの初速が 0 ではなくなっている

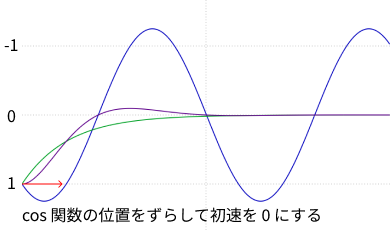
初速を変えるために、cos 関数を移動させます。以下のグラフは初速が 0 となる時のグラフです。cos 関数が初期位置から下方向に伸びています。これが上方向に伸びている指数関数と相殺され、初速が 0 となります。

初速を 0 にするために、cos 関数を平行移動させたグラフ

bounce > 0 の数式の定数を決める #

Animate with springs では使われている数式の紹介はされていますが、数式の中の定数に具体的にどのような値が入るのかは説明されていません。この節では、その定数をどのように決めるればよいかを説明します。bounce > 0 の時の数式を再掲します。

A × cos(a × t + b) × e ^{-c × t}

この式で決める必要のある定数は A, a, b, c の 4 つです（e はネイピア数、t は時間なので決める必要ありません）。まず、c は 0 の時に減衰部分（指数関数）が常に 1 となり、値が大きくなるに連れて減衰の度合いが大きくなっていく値です。これは bounce パラメーターの値にそって自由に決めれば良いです。

また、a はバウンスの周期を決める定数なので、どのようなアニメーションにしたいかによって自由に決められます。

a と c は自由に決めて良いので、本記事では以下のようにします。

a = 1.7 × 𝜋
c = 8 × (1 - bounce)

残るは A と b ですが、この二つは以下の制約から計算によって決まります。

初期位置は常に 1 なので、元の数式に t = 0 を代入して、A × cos(b) = 1
初速が決まっているので、元の数式を微分したものに t = 0 を代入した時の速度 v は、v = -A × (c × cos(b) + a × sin(b))

この2つの式から A と b を求めると以下のようになります。

A = 1 / cos(b)
b = atan2(-c - v, a)

以上の考え方で bounce = 0、bounce < 0 の数式の定数も同様に決められます。

実際に CSS 数式アニメーションで動かす #

前節で決めた定数を使って、前回の記事「CSS 数式アニメーションで初速も考慮できる表現力の高いイージングを書く」で紹介した、数式を CSS に書いてアニメーションする方法でスプリングアニメーションを実装します。

CSS 数式アニメーションで初速も考慮できる表現力の高いイージングを書く

紹介した数式そのままだと、1 から 0 へとアニメーションをすることになるので、実際のアニメーションの初期位置と終了位置を数式に当てはめる必要があります。 紹介したスプリングアニメーションの数式全体を f(t) とおいて、初期位置を from、終了位置を to とすると、以下のように調整することで実際の位置をアニメーションに適用できます。

(from - to) × f(t) + to

また、定数を決める際に触れた初速 v は初期位置 1 終了位置 0 の時に t が 1 増える時にどれだけ値が変わるかを表していて、単位が px / 秒ではないので、初速の単位の変換も行う必要があります。 px / 秒の初速 initial-velocity がある時、それを v に変換する式は以下の通りです。

v = (initial-velocity / (from - to)) × (1000 / duration)

これまでのことをすべて適用し、CSS にすると以下のような実装になります。

.ball {
  width: 50px;
  height: 50px;
  border-radius: 50%;
  background-color: #0a0;
  animation: time calc(3ms * var(--duration)) linear infinite;

  /* 各種パラメーター */
  --from: 0;
  --to: 300;
  --bounce: 0.5;
  --duration: 800;
  --initial-velocity: 0;
  --A: 1 / cos(var(--b));
  --a: 1.7 * pi;
  --b: atan2(-1 * var(--c) - var(--v), var(--a));
  --c: 8 * (1 - var(--bounce));
  --v: (var(--initial-velocity) / (var(--from) - var(--to))) * (1000 / var(--duration));

  /* スプリングアニメーションの数式 */
  /* prettier-ignore */
  translate: calc(
    1px * (
      (var(--from) - var(--to))
      * (var(--A) * cos(1rad * var(--a) * var(--t) + var(--b)) * exp(-1 * var(--c) * var(--t)))
      + var(--to)
    )
  );
}

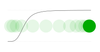
この実装を動かしたものが以下のデモです。記事執筆時点で Chrome と Firefox で実装されていない機能を利用しているため、Safari でのみ動作します。

結論 #

スプリングアニメーションを数式で実装することで、パラメーターが bounce と duration の2つになり、直感的にわかりやすくなりました。ただ、この実装を直接アプリケーションに書くには記述量が多すぎるので、実際の開発ではライブラリにしたものを使うのが良いでしょう。そのライブラリを紹介した記事もあるので、興味があれば読んでみてください。

直感的なオプションでスプリングアニメーションできる JavaScript ライブラリ CSS Spring Animation