
今はなき Tweetbot の至高のインタラクションを高校数学と物理を使って再現する
iOS の Twitter(現X)クライアントに Tweetbot というアプリがありました。全 Twitter クライアントの中でインタラクションの出来が群を抜いており、筆者はこのアプリのインタラクションが気持ち良くて愛用していました。
筆者が Tweetbot のインタラクションの中で最も好きなのが、ツイートの画像タップで拡大表示した後、その画像をドラッグすることで、カードのように画面外に飛ばし、拡大表示を閉じれるというものです。そのカード飛ばしインタラクションを再現したものが以下のデモです。
このインタラクションの気持ち良さは、ただ画像が飛んでいくだけでなく、ドラッグに合わせて自然に画像が回転し、ドラッグ後もくるくると回転しながら飛んでいくところにあります。実装も興味深く、高校数学や物理で学んだことを組み合わせる必要があります。
本記事では、この Tweetbot のカード飛ばしインタラクションの実装について解説します。高校までの数学や物理の話が出てきますが、なるべく図を使い、平易な解説を行います。また、本記事の最後に、このインタラクションの HTML、CSS、JavaScript コードの全体を掲載しています。
カード飛ばしインタラクションの考え方 #
実際に机の上にカード状のものを置き、人差し指でスライドしてみてください。カードは指を動かした分だけ移動し、回転が指を置いた位置を中心に起こります。指がカードの中心から離れた位置にあるほど、回転する角度も大きくなります。
現実世界でカードをスライドした時の挙動を参考にすると、カードの移動については指の移動、つまり、ドラッグの移動と同様に動かせば良さそうです。カードの回転については、ドラッグされた点を中心に行えば良いでしょう。では、回転する角度はどうやって求めるのでしょうか?

物体にどれだけ回転させる力が働いているかを表すものとして、力のモーメントがあります。この値を使うことでカードの回転角度を計算できます。以降の節で、この実装でどのように力のモーメントを求めるかを解説します。
値の定義 #
詳細の解説に入る前に、この実装で使う値の定義を以下に示します。最終的には JavaScript の実装になるため、変数や定数の表現は数学よりも JavaScript に近いものになっています。
bx,by: 画像の左上の座標cx,cy: 画像の中心点x0,y0: ドラッグ開始点x,y: ドラッグ中の座標vy,vx: ドラッグの速度
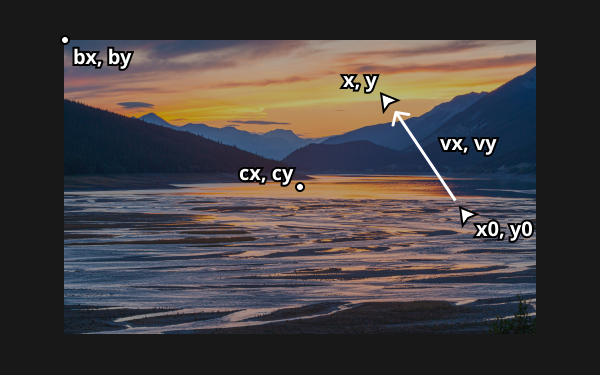
中心からの距離と、掴んだ点に働く力の大きさを求める #
力のモーメント m は以下の式で求められます。
m = r * F * sin𝜃
ただし
r: 画像の中心から力が働く点(ドラッグ点)への距離
F: 力の大きさ
𝜃: 力の方向とrのなす角今回の実装ではドラッグされた距離 d を力の大きさ F の代わりに使います。この関係を図で表すと以下の通りです。
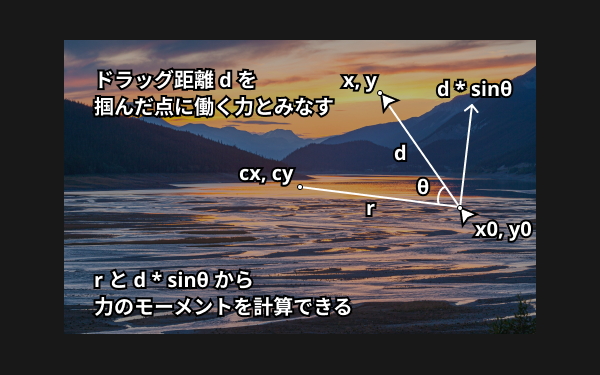
r は中心点 cx, cy と、ドラッグの開始点 x0, y0 を使って以下の式で求められます。
r = √(rx² + ry²)
ただし
rx = x0 - cx
ry = y0 - cyd はドラッグの開始点 x0, y0 と、ドラッグ中の座標 x, y を使って以下の式で求められます。
d = √(dx² + dy²)
ただし
dx = x - x0
dy = y - y0角度 𝜃 を2直線のなす角と考えて求める #
残る 𝜃 は (cx, cy) と (x0, y0) を通る直線、(x0, y0) と (x, y) を通る直線のなす角として求められます。2つの直線は以下の式で表せます。
y = (ry / rx) * x –– (cx, cy) と (x0, y0) を通る直線
y = (dy / dx) * x –– (x0, y0) と (x, y) を通る直線
ここで、タンジェントは直線の傾きと等しいので以下のようにおきます。
tan𝛼 = ry / rx
tan𝛽 = dy / dx𝛼 と 𝛽 はそれぞれの直線と x 軸の正の向きとのなす角なので、2直線のなす角 𝜃 = 𝛼 - 𝛽 となります。

ここでタンジェントの加法定理に上記の tan𝛼 と tan𝛽 を代入し、式を整理することで、以下が成り立ちます。
tan(𝛼 - 𝛽) = (rx * dy - dx * ry) / (rx * dx + ry * dy)求めたいのは 𝜃 = 𝛼 - 𝛽 なので、アークタンジェント2(atan2)を使って以下のように求められます。
𝜃 = atan2(rx * dy - dx * ry, rx * dx + ry * dy)力のモーメントを使って回転する角度を決める #
これで力のモーメント m を求めるために必要な値 r, d, 𝜃 が求まりました。次はこれらを用いて、回転する角度を決めます。
力のモーメントは物体を回転させる量を表しているだけで、具体的な角度までは定められていません。なので、m に適当な重み定数 w をかけ合わせることで、回転する角度を決めます。今回は w = 0.0005 とすることで自然な回転量となりました。
回転の角度を CSS の rotate に設定するとともに、先ほどまでの計算の過程で得られた dx, dy(ドラッグされた距離)を translate に設定して平行移動も行います。

マウスでドラッグされている点を回転の中心にするには transform-origin に x0, y0 の値を指定します。以下は画像の要素に CSS をセットする JavaScript コードです。
// 力のモーメントから角度に変換する時の重み定数
const w = 0.0005
// ドラッグによって生じる平行移動と回転
function transform() {
const translate = `translate(${dx()}px, ${dy()}px)`
const rotate = `rotate(${m() * w}deg)`
return translate + ' ' + rotate
}
// ドラッグしている点を回転の中心にする
function transformOrigin() {
return `${x0 - bx}px ${y0 - by}px`
}
// ドラッグ中のスタイルをセットする
function setStyle() {
image.style.transform = transform()
image.style.transformOrigin = transformOrigin()
}
カードが画面外に飛ばされる判定とアニメーションの実装 #
ここまででカードをドラッグすると移動とともに回転するインタラクションが実装できました。この節ではカードを勢いよくドラッグした時に、画面外に飛んでいくアニメーションを実装します。
まず、ドラッグを終えた瞬間に、カードが画面外に完全に飛ばされるほどの勢いがあるかどうかを判定する必要があります。もし十分な勢いがなければ、カードを元の位置に戻し、勢いがあれば、カードを画面外に飛ばすアニメーションを実行するという条件分岐を行うためです。
この判定を行うために、ここまで飛べばカードが完全に画面から見えなくなるだろうという境界 boundary を定義します。そして、ドラッグ座標 x, y とドラッグの速度 vx, vy から、最終的にカードがどこまで飛んでいくかを計算し、結果の座標が boundary を越えるかどうかをチェックします。
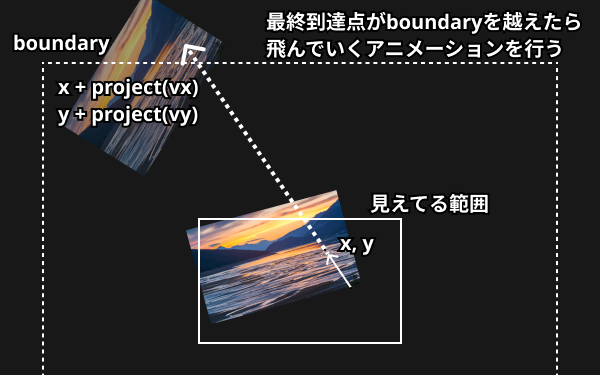
カードがどこまで飛んでいくかを計算する方法には、Designing Fluid Interfaces で紹介されている project 関数が使えます。project 関数の実装は以下の通りです。
// 慣性力が減衰する度合い
// 値が0に近いほど大きく減衰する
const decelerationRate = 0.9988
// 速度 initialVelocity の時に最終的にどれだけ移動するかを計算する
function project(initialVelocity) {
return (initialVelocity / 1000) * (decelerationRate / (1 - decelerationRate))
}
この project 関数をドラッグ終了時に使い、カードがどこまで飛んでいくかを計算します。計算するだけで実際のアニメーションはまだ行いません。boundary は wrapper の座標(見えている範囲)から画像の長い方の辺の長さを外側に足したものにします。最後に project で計算した座標が boundary を越えていれば、カードを画面外に飛ばすアニメーション startMomentum を実行します。
function onDragEnd() {
if (!dragging) {
return
}
dragging = false
// 速度 vx, vy でカードを飛ばした時に、最終的に移動する座標を計算する
const projectedX = x + project(vx)
const projectedY = y + project(vy)
const imageBounds = image.getBoundingClientRect()
const imageLongerEdge = Math.max(imageBounds.width, imageBounds.height)
const wrapperBounds = wrapper.getBoundingClientRect()
// カードが画面外に飛ばされたとみなす境界
// 今回は実装を簡単にするため、画像の長い方の辺の長さを wrapper の外側に足した座標を境界とする
const boundary = {
left: wrapperBounds.left - imageLongerEdge,
right: wrapperBounds.right + imageLongerEdge,
top: wrapperBounds.top - imageLongerEdge,
bottom: wrapperBounds.bottom + imageLongerEdge,
}
// project で計算した座標が境界外にあるかどうかを判定
if (
projectedX < boundary.left ||
projectedX > boundary.right ||
projectedY < boundary.top ||
projectedY > boundary.bottom
) {
// 境界外にある場合はカードを飛ばすアニメーションを開始
startMomentum(boundary)
} else {
// 境界を出ていない場合はカードを元に戻す
cancel()
}
}
startMomentum 関数の中では実際にカードを飛ばすアニメーションを実行します。vx, vy に対して project 関数でも使っている decelerationRate を適用し、速度が段々と小さくなるようにします。更新後の vx, vy を使って次の x, y 座標を計算し、画像要素の CSS に適用します。最後に、速度が十分小さくなるか、画像が画面外に出て、かつアニメーションの開始から1秒以上経過していたら、アニメーションを終了させます。
function startMomentum(boundary) {
let startTimestamp
let lastTimestamp
function momentum(timestamp) {
if (!lastTimestamp) {
// 初回の呼び出し時は開始時間を記録するだけで処理を行わない
startTimestamp = timestamp
} else {
const duration = timestamp - lastTimestamp
// project 関数で使っている定数をここで使い、経過時間によって速度を減衰させる
vx = vx * decelerationRate ** duration
vy = vy * decelerationRate ** duration
// 速度に応じてカードを移動させる
x += vx * (duration / 1000)
y += vy * (duration / 1000)
// CSS を適用
setStyle()
// 移動後の座標が boundary の外にあるかどうかを判定
const imageDisappeared =
x < boundary.left ||
x > boundary.right ||
y < boundary.top ||
y > boundary.bottom
// 速度が十分小さくなっているかどうかを判定
const almostStopped = Math.abs(vx) < 1 && Math.abs(vy) < 1
// 速度が十分小さいか、画像が画面外に出ていて、
// アニメーションの開始から1秒以上経過していたらアニメーションを終了する
if (
almostStopped ||
(imageDisappeared && timestamp - startTimestamp > 1000)
) {
// 本来のアプリではここで画像ポップアップを閉じる処理を入れるべきだが、
// 今回はデモなので画像を元の位置に戻すだけにする
image.style.transform = ''
return
}
}
// 次のフレームへとループさせる
lastTimestamp = timestamp
requestAnimationFrame(momentum)
}
requestAnimationFrame(momentum)
}
本来のアプリでは、このインタラクションはツイート画像の拡大ポップアップに実装されていて、アニメーションの終了時にポップアップを閉じる処理が入ります。今回はデモなので、画像を元の位置に戻すだけにしています。
これでカード飛ばしインタラクションが完成しました。完成したデモ(本記事の最初のデモと同じ)と、完全版のコードを見てみましょう。
カード飛ばしインタラクションの完成版のコード
<div id="wrapper">
<img
id="image"
src="/img/QfjbHk_Vue-600.jpeg"
width="600"
height="375"
/>
</div>const wrapper = document.getElementById('wrapper')
const image = document.getElementById('image')
// ドラッグ開始点
let x0 = 0
let y0 = 0
// ドラッグ中の座標
let x = 0
let y = 0
// ドラッグの速度
let vx = 0
let vy = 0
// 画像の左上の座標
let bx = 0
let by = 0
// 画像の中心点
let cx = 0
let cy = 0
let dragging = false
// 前回のドラッグイベントとそのタイムスタンプ
let prevDrag = null
// ドラッグ開始点と画像の中心点の距離
const rx = () => x0 - cx
const ry = () => y0 - cy
const r = () => Math.sqrt(rx() ** 2 + ry() ** 2)
// ドラッグの距離
const dx = () => x - x0
const dy = () => y - y0
const d = () => Math.sqrt(dx() ** 2 + dy() ** 2)
// 力のモーメントを求めるのに必要な2直線のなす角
const angle = () =>
Math.atan2(rx() * dy() - dx() * ry(), rx() * dx() + ry() * dy())
// 力のモーメント
const m = () => r() * d() * Math.sin(angle())
// 力のモーメントから角度に変換する時の重み定数
const w = 0.0005
// ドラッグによって生じる平行移動と回転
function transform() {
const translate = `translate(${dx()}px, ${dy()}px)`
const rotate = `rotate(${m() * w}deg)`
return translate + ' ' + rotate
}
// ドラッグしている点を回転の中心にする
function transformOrigin() {
return `${x0 - bx}px ${y0 - by}px`
}
// ドラッグ中のスタイルをセットする
function setStyle() {
image.style.transform = transform()
image.style.transformOrigin = transformOrigin()
}
// 慣性力が減衰する度合い
// 値が0に近いほど大きく減衰する
const decelerationRate = 0.9988
// 速度 initialVelocity の時に最終的にどれだけ移動するかを計算する
function project(initialVelocity) {
return (initialVelocity / 1000) * (decelerationRate / (1 - decelerationRate))
}
// ドラッグ開始
function onDragStart(event) {
event.preventDefault()
event.currentTarget.setPointerCapture(event.pointerId)
dragging = true
// キャンセル処理を取り消す
image.classList.remove('cancelling')
const { pageX, pageY } = event
x0 = x = pageX
y0 = y = pageY
const imageBounds = image.getBoundingClientRect()
bx = imageBounds.left
by = imageBounds.top
cx = bx + imageBounds.width / 2
cy = by + imageBounds.height / 2
}
// ドラッグ移動中
function onDragMove(event) {
if (!dragging) {
return
}
const { pageX, pageY } = event
x = pageX
y = pageY
setStyle()
const now = Date.now()
// 前回のドラッグイベントからドラッグの移動速度を求める
if (prevDrag) {
const prevX = prevDrag.event.pageX
const prevY = prevDrag.event.pageY
const duration = (now - prevDrag.timestamp) / 1000
if (duration !== 0) {
vx = (x - prevX) / duration
vy = (y - prevY) / duration
}
}
prevDrag = {
event,
timestamp: now,
}
}
function onDragEnd() {
if (!dragging) {
return
}
dragging = false
// 速度 vx, vy でカードを飛ばした時に、最終的に移動する座標を計算する
const projectedX = x + project(vx)
const projectedY = y + project(vy)
const imageBounds = image.getBoundingClientRect()
const imageLongerEdge = Math.max(imageBounds.width, imageBounds.height)
const wrapperBounds = wrapper.getBoundingClientRect()
// カードが画面外に飛ばされたとみなす境界
// 今回は実装を簡単にするため、画像の長い方の辺の長さを wrapper の外側に足した座標を境界とする
const boundary = {
left: wrapperBounds.left - imageLongerEdge,
right: wrapperBounds.right + imageLongerEdge,
top: wrapperBounds.top - imageLongerEdge,
bottom: wrapperBounds.bottom + imageLongerEdge,
}
// project で計算した座標が境界外にあるかどうかを判定
if (
projectedX < boundary.left ||
projectedX > boundary.right ||
projectedY < boundary.top ||
projectedY > boundary.bottom
) {
// 境界外にある場合はカードを飛ばすアニメーションを開始
startMomentum(boundary)
} else {
// 境界を出ていない場合はカードを元に戻す
cancel()
}
}
function startMomentum(boundary) {
let startTimestamp
let lastTimestamp
function momentum(timestamp) {
if (!lastTimestamp) {
// 初回の呼び出し時は開始時間を記録するだけで処理を行わない
startTimestamp = timestamp
} else {
const duration = timestamp - lastTimestamp
// project 関数で使っている定数をここで使い、経過時間によって速度を減衰させる
vx = vx * decelerationRate ** duration
vy = vy * decelerationRate ** duration
// 速度に応じてカードを移動させる
x += vx * (duration / 1000)
y += vy * (duration / 1000)
// CSS を適用
setStyle()
// 移動後の座標が boundary の外にあるかどうかを判定
const imageDisappeared =
x < boundary.left ||
x > boundary.right ||
y < boundary.top ||
y > boundary.bottom
// 速度が十分小さくなっているかどうかを判定
const almostStopped = Math.abs(vx) < 1 && Math.abs(vy) < 1
// 速度が十分小さいか、画像が画面外に出ていて、
// アニメーションの開始から1秒以上経過していたらアニメーションを終了する
if (
almostStopped ||
(imageDisappeared && timestamp - startTimestamp > 1000)
) {
// 本来のアプリではここで画像ポップアップを閉じる処理を入れるべきだが、
// 今回はデモなので画像を元の位置に戻すだけにする
image.style.transform = ''
return
}
}
// 次のフレームへとループさせる
lastTimestamp = timestamp
requestAnimationFrame(momentum)
}
requestAnimationFrame(momentum)
}
// 元の位置に画像を戻すアニメーションをする
function cancel() {
image.style.transform = ''
image.classList.add('cancelling')
image.addEventListener('transitionend', () => {
image.classList.remove('cancelling')
})
}
// モバイル端末でスクロールさせないようにする
wrapper.addEventListener('touchstart', (event) => {
event.preventDefault()
})
wrapper.addEventListener('pointerdown', onDragStart)
wrapper.addEventListener('pointermove', onDragMove)
wrapper.addEventListener('pointerup', onDragEnd)
wrapper.addEventListener('pointercancel', onDragEnd)body {
background-color: #181818;
}
#wrapper {
overflow: hidden;
position: absolute;
inset: 0;
}
#image {
position: absolute;
left: 0;
right: 0;
top: 0;
bottom: 0;
margin: auto;
max-width: 100%;
max-height: 100%;
width: auto;
height: auto;
}
#image.cancelling {
transition: transform 0.5s cubic-bezier(0.15, 0.5, 0.6, 0.9);
}結論 #
Tweetbot のカード飛ばしインタラクションは使っていて気持ちの良いもので、しかも、使い勝手を悪くしない秀逸なものでした。インタラクションの実装にこだわることには、ビジネス的なメリットを説明しづらく、こういったインタラクションはあまり見かけることがありません。しかし、日々使うアプリのインタラクションにおいては、使うことによる気持ち良さがユーザーの継続利用したい気持ちに大きく寄与すると思います。実際に、筆者は Tweetbot のインタラクションの気持ち良さによって継続利用していました。本記事で解説したような手間のかかるインタラクションの実装をできるようになっておくのは、選択肢として良いかもしれません。